Merge Sort

2024년 1월 28일 작성

합병정렬, 말그대로 부분으로 쪼갠뒤, 합치면서 정렬하는 기법이다. 그림을 보면 이해가 쉽다. 처음부터 원소하나까지 쪼개질 때까지는 정렬이 일어나지 않는다. 그다음 쪼개졌던 리스트들을 새 리스트에 합치면서 정렬한다.

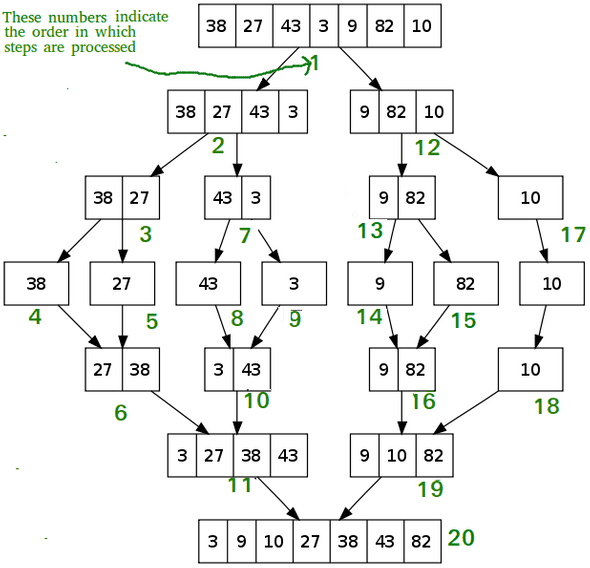출처: 여기

부분문제로 나누어 해결하는 기법 -> 분할 정복 알고리즘 종류 중 하나이다.

시간/공간 복잡도

트리를 생각하며 시간복잡도를 계산해보자.

정렬하는 리스트의 길이를 n이라하고 요소끼리 비교하는 데 걸리는 시간을 O(c) 라고 하자.

분할 단계와 병합 단계를 나눠 시간복잡도를 합할 것이다.

1. 분할 단계: 배열을 1개의 요소가 남을 때까지 반으로 계속 쪼갠다. -> O(1) * log(n) 반으로 쪼개는것은 실제 배열을 새로 생성하는 것이 아니라, 인덱스를 조정하는 것이므로 O(1)으로 계산한다.

2. 병합 단계 전제: 두 개의 서브배열은 이미 정렬되어 있고, 각 서브배열의 크기가 l 이라고하자.

   병합 시간복잡도 병합 단계에서는 두 개의 서브배열을 비교하며 합치는 연산을 한다.
   

   비교연산 시간복잡도 (1) 두 서브 배열을 병합할 때, 최대 2l 번비교하게 된다.
   (2) 이러한 서브배열 쌍의 갯수를 고려했을 때, 한 높이에서의 비교연산은 총 n번임을 할 수 있다.
   (3) 비교 연산의 시간복잡도가 O(m) 이라고 한다면, 한 높이에서의 비교연산 시간복잡도는 O(m*n)이다.
   (4) 각 높이마다 비교연산의 횟수는 같으므로 높이 log n 을 곱하면 O(m*n*logn)
   

3. 총 시간복잡도 O(log n) + O(m*n*log n) = O(m*n*log n)

참고 - 두 서브배열을 합칠 때 비교하는 횟수 : 예를 들어, L과 R 을 각각의 길이가 n/2인 배열이라 가정합시다. 병합 과정에서는 L의 요소와 R의 요소를 비교하여 더 작은 요소를 결과 배열에 추가합니다. 각 비교 후에는 L 또는 R에서 한 요소가 결과 배열로 이동합니다. 따라서, L과 R의 모든 요소를 한 번씩 비교하고 결과 배열로 옮기기 위해 최대 n번의 비교가 필요합니다. (n/2 + n/2 = n)

pseudo code

개인적으로는 수도코드 코드를 꼼꼼히 이해하는 것보다는 전체적인 흐름만 참고하여 코드를 작성해보는 것이 좋다고 생각했다. 참고차 수도코드에서 사용한 파라미터와 함수 설명을 추가.

파라미터 설명

• A: 정렬 대상이 되는 리스트
• p: list의 첫번째 index
• q: list의 중간 index
• r: list의 마지막 index

함수

• MERGE-SORT(A,p,r): 정렬 전, 리스트를 분할하는 역할
• MERGE(A,p,q,r): p~q 까지 정렬된 리스트와 q+1부터 r까지 정렬된 리스트를 합쳐 다시 정렬한다.

java 코드

---

미래의 나에게: 시간복잡도를 구하는 것을 헷갈려했으니 반드시 그림을 그리며 복기해보길!